KMP算法

KMP算法

KMP:一个人能走的多远不在于他在顺境时能走的多快，而在于他在逆境时多久能找到曾经的自己。——某位哲学大师(雾)

上面这句话很直观的体现了kmp算法的一个重要的特点：前后缀比较。比如我们看下面这道例题：

找出字符串中第一个匹配项的下标

给你两个字符串 haystack 和 needle ，请你在 haystack 字符串中找出 needle 字符串的第一个匹配项的下标（下标从 0 开始）。如果 needle 不是 haystack 的一部分，则返回 -1 。

示例 1：

输入：haystack = "abxabcabcaby", needle = "abcaby"
输出：6
解释："abcaby" 在下标 6 处匹配。

示例 2：

输入：haystack = "leetcode", needle = "leeto"
输出：-1
解释："leeto" 没有在 "leetcode" 中出现，所以返回 -1 。

提示：

• 1 <= haystack.length, needle.length <= 104
• haystack 和 needle 仅由小写英文字符组成

普通暴力解法

最直观的解法就是双循环，把haystack里面的字符都遍历一遍，然后再看这个字符后面是不是和needle匹配的，要是有不匹配的，直接break。

class Solution {
    public int strStr(String haystack, String needle) {
        if (needle.length() == 0) {
            return 0; // 如果 needle 是空字符串，则返回 0
        }
        if (haystack.length() < needle.length()) {
            return -1; // 如果 haystack 比 needle 短，则不能包含 needle
        }

        for (int i = 0; i <= haystack.length() - needle.length(); i++) {
            int j;
            for (j = 0; j < needle.length(); j++) {
                if (haystack.charAt(i + j) != needle.charAt(j)) {
                    break; // 如果字符不匹配，退出内层循环
                }
            }
            if (j == needle.length()) {
                return i; // 如果完整匹配，返回起始位置
            }
        }

        return -1; // 如果没有找到 needle，返回 -1
    }
}

可以看到这里套了双层循环，假设m=haystack.length() - needle.length() ,n=needle.length()那么时间复杂度是O(mn)。但是如果我们使用kmp算法，就可以让时间复杂度控制到O(m+n)。

KMP

思路

我们想想当在字符串比较的时候，什么操作是多余的操作？

text: abxabcabcaby
pattern: abcaby

以上述例子比较的时候可以发现：在text的[3:7]部分是和pattern[0:4]部分是重合的，由于最后一个y和text中的下一个c没对上，所以没有配对成功，但是在pattern这部分前面的[0:4]中前缀”ab”和后缀的”ab”是一样的，说明我们只需要重新比较text中[6:7]这个”ab”后面的与pattern[0:1]这个”ab”后面的即可，不用再重新比较”ab”。这样就可以优化算法。

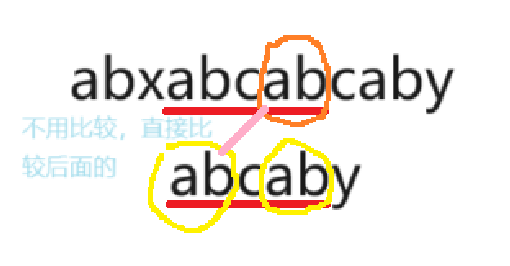
next表

为了方便我们这样索引，我们将要建立一个next表，里面记录的是由后缀到前缀的索引值，也就是说当我们匹对字符串的时候，如果发现不对，那只需要通过索引值跳到需要比较的部分。

建立思路

首先我们给pattern字符串前面加上一个哨兵空字符，为什么要加这个呢？这里是由于之后我们比较的时候如果指针指的字符不匹配，那么我们就要找到指针前面那个字符的所对应的索引值，如果我们加上一个哨兵，那就可以每次不用指针减一，直接j就可以(有点拗口，之后看图会清楚点)。

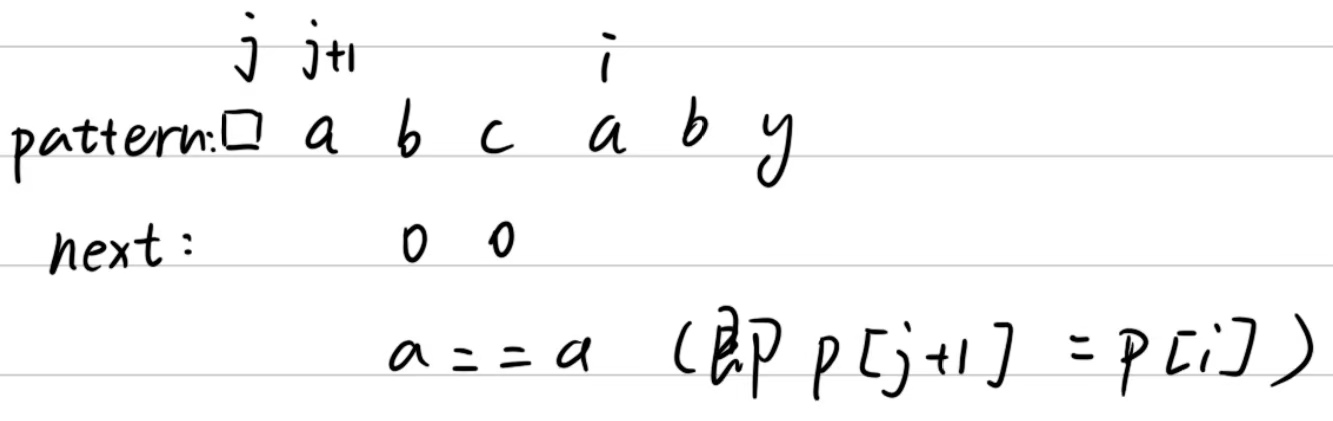
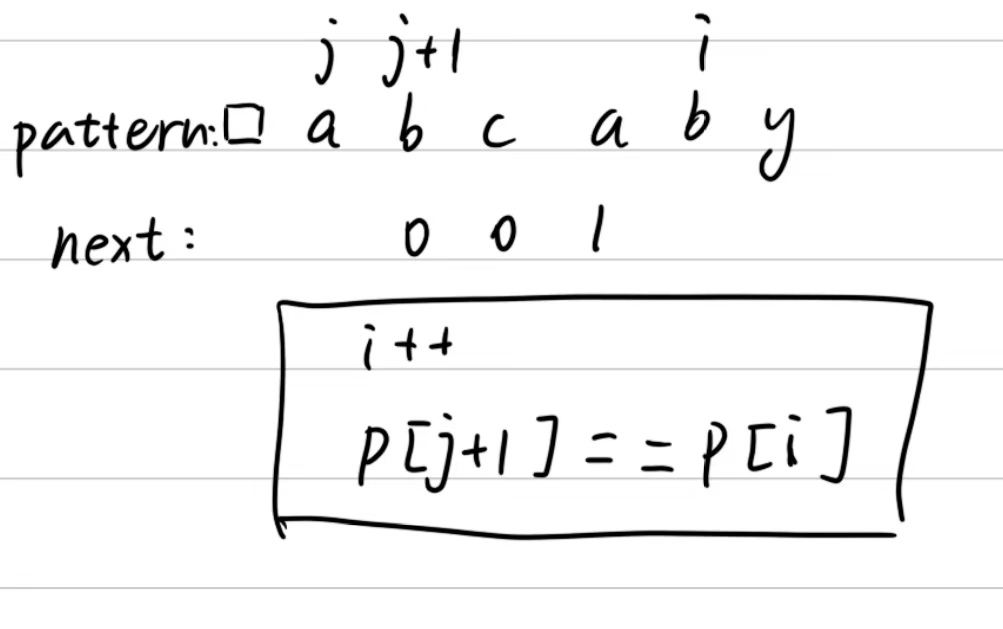
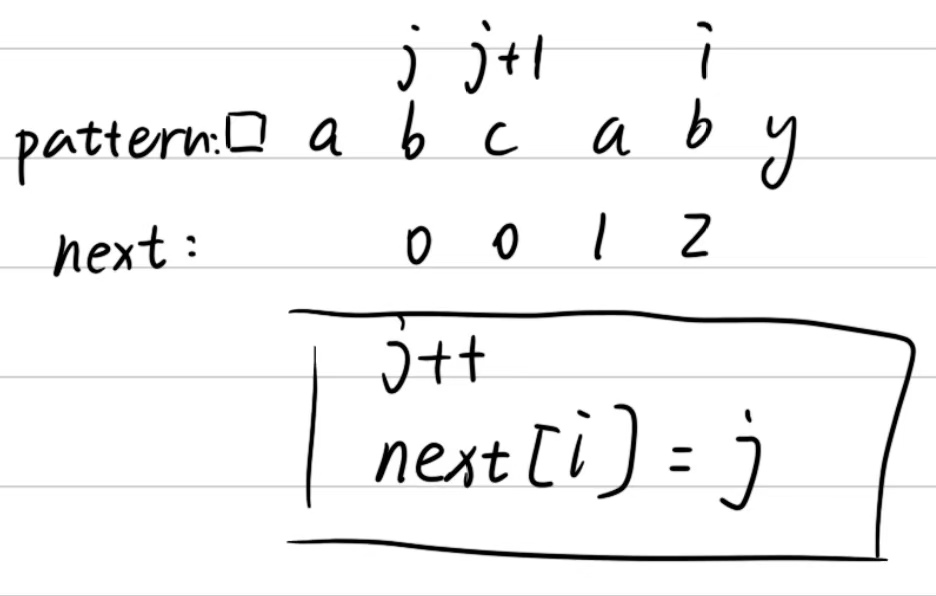
以上就是next表创建的手画过程，用代码来写就是这样：

for(int i=2, j=0;i<=m;i++){ //p就是pattern的缩写，通过toCharArray()来变成字符数组
    while(j>0 && p[j+1] != p[i]) j = next[j]; //如果对不上，就让j不断往前找，直到找到能对上的数
    if(p[j+1] == p[i]) j++; //如果对上了，就让j向后移动一位
    next[i] = j; //next赋值操作
}

可以看到i就是从2开始的，所以我在途中所以为1的地方就没有写值。

与字符串开始匹配

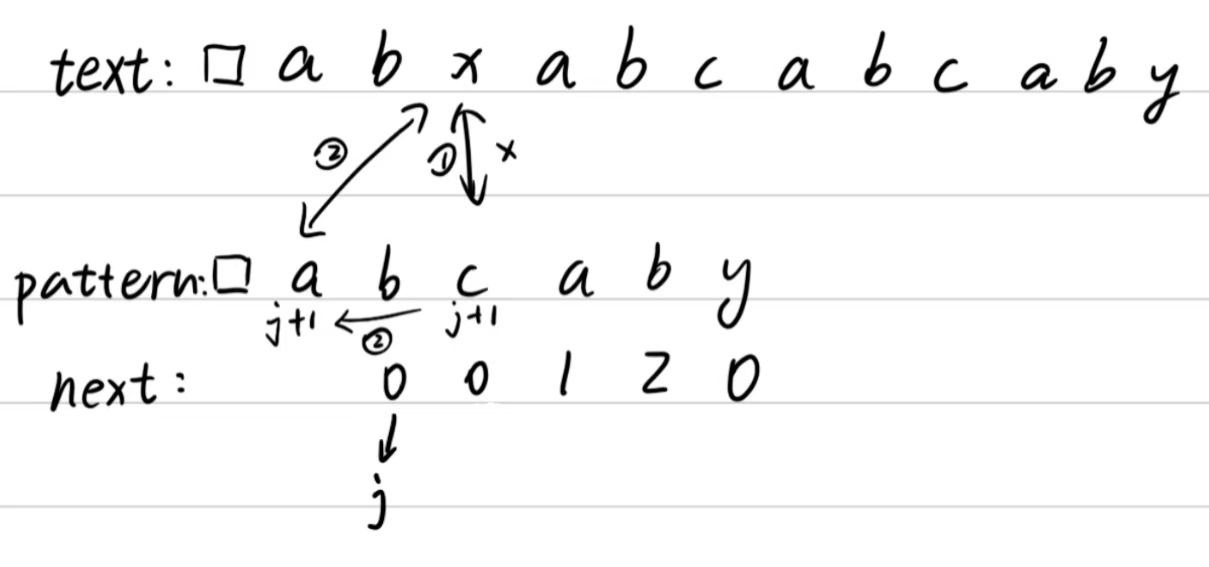
这里发现无法匹配后就直接通过b的前一个字符(a)的索引来向前找有没有为”x”的字符(然而没有)，于是j就停在哨兵字符上。

发现不符，j不动(因为j已经是最上面了，找不上去了)，text中的字符再往后面找。然后重复上面的步骤不停往后比对。最后发现”y”和⑥的”c”不符，于是乎j就往下找(此时j下面的索引为2，因此j跳到”b”上，j+1为”c”)，此时我们就只需要比较”c”和text后面的值了(因为我们知到了”ab”肯定是一样的，不用再比较了)。

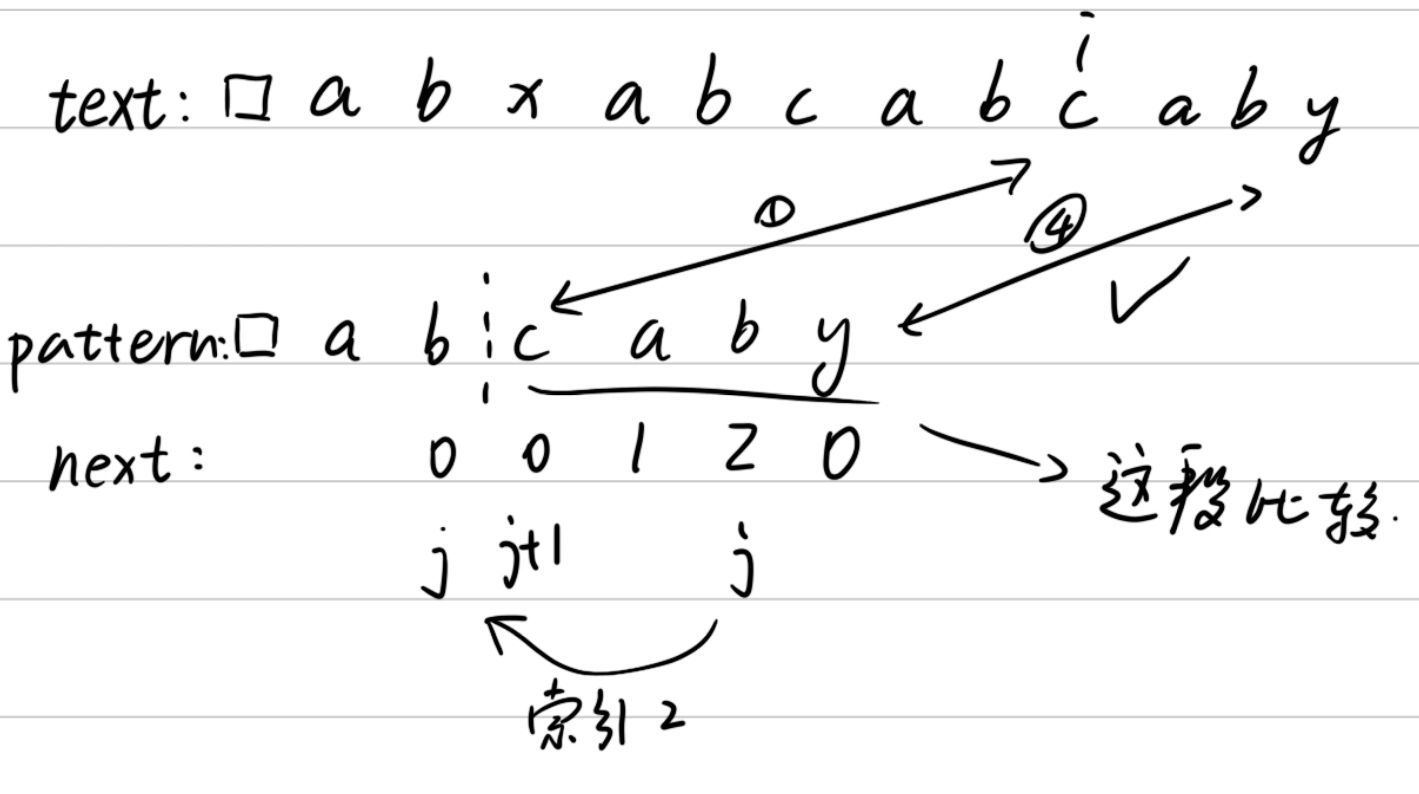
这一步就是kmp算法的核心，有了上面这个思路我们就可以解决上面的例题了。

class Solution {
    public int strStr(String ss, String pp) {
        if (pp.isEmpty()) return 0;
        int n = ss.length(), m = pp.length(); //注意长度的取值是在加入哨兵之前的
        ss = " " + ss; //加入哨兵
        pp = " " + pp;
        char[] s = ss.toCharArray(); 
        char[] p = pp.toCharArray();
        int[] next = new int[m + 1]; //创建next表
        
        for(int i=2, j=0;i<=m;i++){ //填写next表
            while(j>0 && p[j+1] != p[i]) j = next[j]; //找不到的情况，让"j"往前找
            if(p[j+1] == p[i]) j++; //核对成功"j"往前走
            next[i] = j; //将目前这个下标的值改成此时"j"的值
        }

        for(int i=1,j=0;i<=n;i++){ //核对字符
            while(j>0 && s[i] != p[j+1]) j = next[j]; //找不到的情况，让"j"往前找
            if(p[j+1] == s[i]) j++; //核对成功往前走
            if(j == m){ //长度相等就return
                return i - m; //输出第一个元素下标
            }
        }
        
        return -1;
    }
}