并查集

并查集

并查集其实解决的内容就是类似于集合合并的问题，然而如果用普通的数组去储存一个集合若数据量大，不仅调用时占用内存空间大，而且不便于插入或查询操作，因此引入并查集可以很好的解决这点。

功能

1.将两个集合合并

2.询问两个元素是否再一个集合当中

思路

理解这个问题就需要把集合给看成一个树，然后这个树的树根就代表这个集合。当想询问其中一个节点时，我们只要访问这个节点father，然后再找这个father的grandfather直到到树根，就能确定这个点的树根。

//p[x]表示x的父节点
if(p[x]==x) //判断树根
while(p[x]!=x) x=p[x] //求x的集合编号

合并两个集合

合并集合只需要将其中一个集合的树根的编号改成另一个集合的根。

p[x]=y//px是x的集合编号，py是y的集合编号

(俗称：给x的祖宗又认了一个爹)

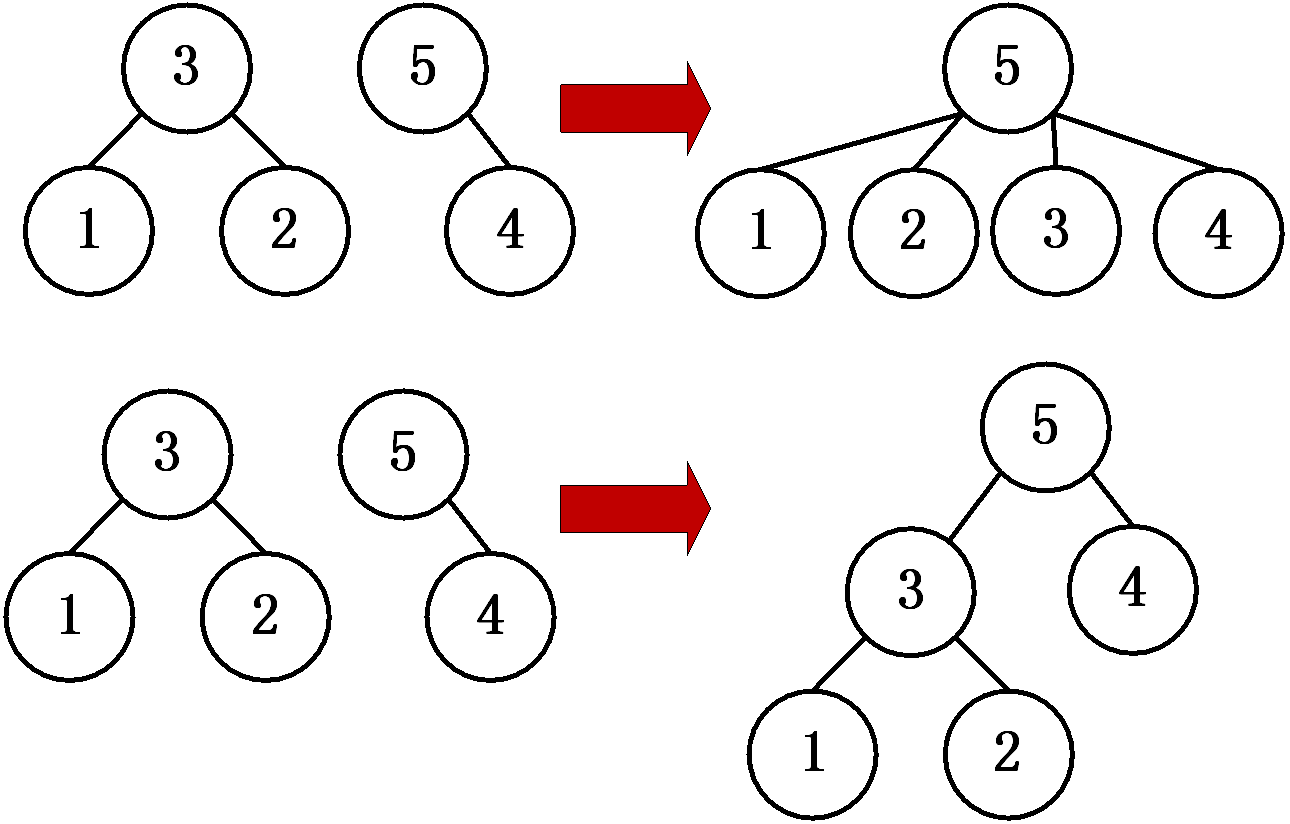
路径压缩

当你找到这个节点的根节点时，就把这些节点的父亲全部变成根节点的编号，也就是让这些节点全部指向根节点。当实现了这个操作后，其查询操作直接将时间复杂度变成O(1)。

int find(int x){ //寻找根+路径压缩
    if(p[x]!=x) p[x]=find(p[x]);
    return p[x];
}

例题

1.合并集合

一共有 n𝑛 个数，编号是 1∼n1∼𝑛，最开始每个数各自在一个集合中。

现在要进行 m𝑚 个操作，操作共有两种：

1. M a b，将编号为 a𝑎 和 b𝑏 的两个数所在的集合合并，如果两个数已经在同一个集合中，则忽略这个操作；
2. Q a b，询问编号为 a𝑎 和 b𝑏 的两个数是否在同一个集合中；

输入格式

第一行输入整数 n𝑛 和 m𝑚。

接下来 m𝑚 行，每行包含一个操作指令，指令为 M a b 或 Q a b 中的一种。

输出格式

对于每个询问指令 Q a b，都要输出一个结果，如果 a𝑎 和 b𝑏 在同一集合内，则输出 Yes，否则输出 No。

每个结果占一行。

数据范围

1≤n,m≤1051≤𝑛,𝑚≤105

输入样例：

4 5
M 1 2
M 3 4
Q 1 2
Q 1 3
Q 3 4

输出样例：

Yes
No
Yes

题解

#include <bits/stdc++.h>
using namespace std;
int p[100005];
int find(int x){ //核心函数，find(x)最终返回值就是x的根节点编号
    if(x!=p[x]) p[x]=find(p[x]);
    return p[x];
}

int main(){ 
    int n,m,a,b;
    string s;
    cin>>n>>m;
    for(int i=0;i<=n;i++){
        p[i]=i;
    }
    while(m--){
        cin>>s>>a>>b;
        if(s=="M"){
            p[find(a)]=find(b);//让a根节点的父亲变成b节点的根节点
        }
        else if(s=="Q"){
            if(find(a)==find(b)){ //判断两个数是不是属于同一个集合，其实就是两个根编号是不是一样
                cout<<"Yes"<<endl;
            }
            else{
                cout<<"No"<<endl;
            }
        }
    }
}

2.合并根

题目描述

w 星球的一个种植园，被分成 m×n 个小格子（东西方向 m 行，南北方向 n 列）。每个格子里种了一株合根植物。

这种植物有个特点，它的根可能会沿着南北或东西方向伸展，从而与另一个格子的植物合成为一体。

如果我们告诉你哪些小格子间出现了连根现象，你能说出这个园中一共有多少株合根植物吗？

输入格式

第一行，两个整数 m，n，用空格分开，表示格子的行数、列数（1<m,n<1000）。

接下来一行，一个整数 k，表示下面还有 k 行数据(0<k<1e5)。

接下来 k 行，每行两个整数 a，b，表示编号为 a 的小格子和编号为 b 的小格子合根了。

格子的编号一行一行，从上到下，从左到右编号。

比如：5×4 的小格子，编号：

1  2  3  4
5  6  7  8
9  10 11 12
13 14 15 16
17 18 19 20

输出格式

一行一个整数，表示答案

输入样例

5 4
16
2 3
1 5
5 9
4 8
7 8
9 10
10 11
11 12
10 14
12 16
14 18
17 18
15 19
19 20
9 13
13 17

输出样例

5

题解：

#include<bits/stdc++.h>
using namespace std;
int p[1000005],vis[1000005];

int find(int x){ //寻找根
    if(p[x]!=x) p[x]=find(p[x]);
    return p[x];
}

int main(){
    int n,m,k,a,b,sum=0;
    cin>>n>>m;
    cin>>k;
    for(int i=1;i<=n*m;i++) p[i]=i;
    while(k--){
        cin>>a>>b;
        p[find(a)]=find(b);//合并集合
    }
    
    for(int i=1;i<=n*m;i++){
        // cout<<p[i]<<" ";
        if(i==p[i])sum++;
    }
    cout<<sum;
}

这题使用并查集解题，核心主要两个步骤：寻找该元素的根、合并两个集合

然后最后判断是用if(i==p[i])来判断这里的根有几个，因为我们知道只有p[x]==x时，才是这个树的根(因为在数组上理解就是所有的数字比如：[-1，1，2，3，4] —> [ -1，4，2，1，3]，我们可以发现数组的顺序表示数字，而对应上面的数字就是其根的索引，在并查集的操作下只有根节点是i==p[i]，因此我们也可以将其作为判断几个集合的依据)。